Network Architecture Topologies

Network Architecture Topologies

HPC uses a lot of components (caches, processors, servers, …) which need to communicate

• This is done using networks
• In this lecture we want to look at fundamentals of networks
• Understanding networks will allow you to design efficient communication schemes (later lectures)

What is a Interconnection Network?

Digital System is composed of three components:

• Logic → produce new data
• Memory → move data in time
• Communication → move data in space

Most systems performance is limited by communication!

• Why?

Interconnection networks are used to move data between the subsystems of a digital system:

• CPUs and caches
• Caches and memory banks
• Nodes in a supercomputer
• Your desktop and Youtube servers

What defines an interconnection network?

How to evaluate an interconnection network?

1. Cost
2. Latency
3. Reliability
4. Power Consumption
5. Bandwidth Bisection

And many more…

Intro to Network Topologies

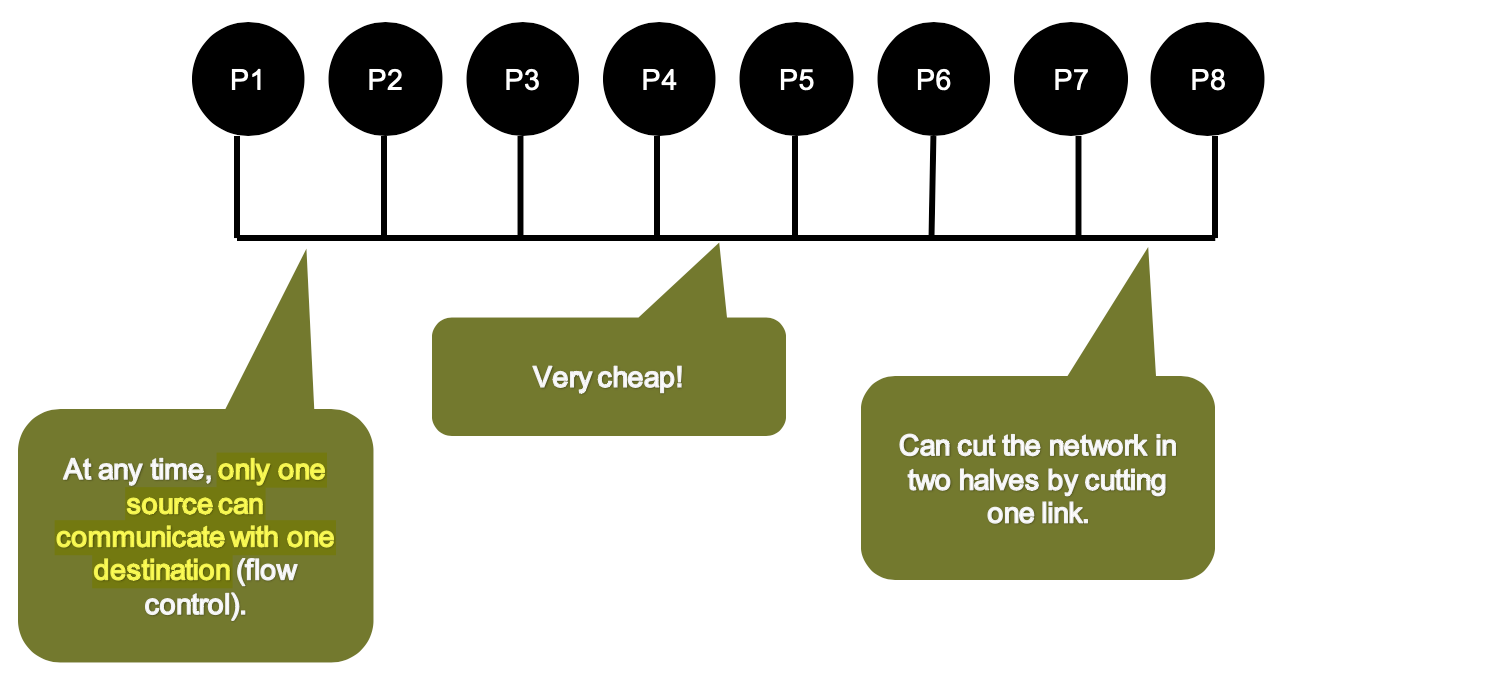
Bus

At any time, only 1 source can communicate with 1 destination.

• It’s very cheap
• We can cut the network in half by cutting one link
  • Single point of failure

Property	Value
Degree	$1, 2$
Diameter	$N-1$
Total links	$N-1$
Bisection Bandwidth	$1$

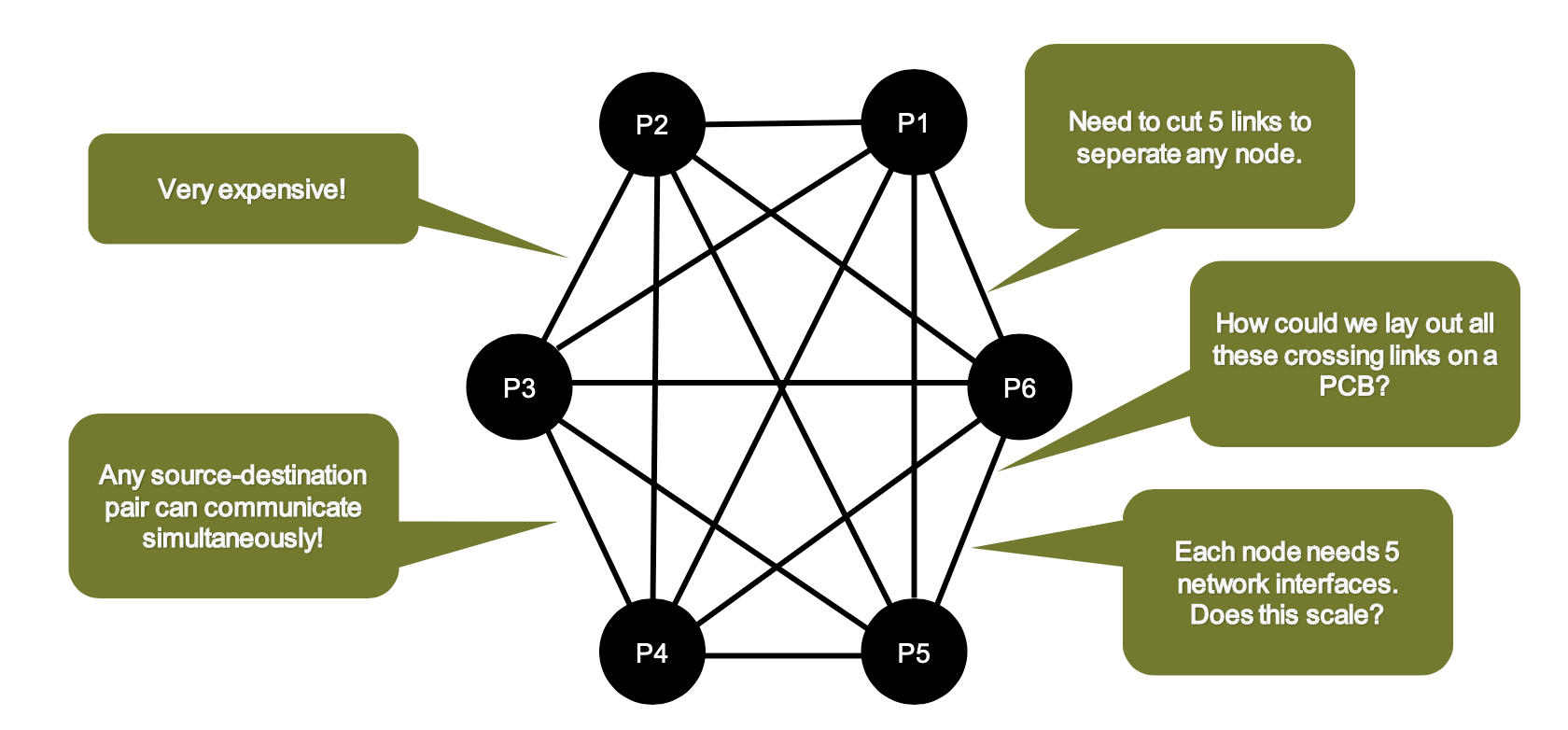
Fully Connected

Any source-destination pair can communicate at any time. However, it’s very expensive because it has $O(N^2)$ links, since each node requires $N-1$ interfaces.

It doesn’t scale

Property	Value
Degree	$N-1$
Diameter	$1$
Total links	$\frac {N(N-1)} 2$
Bisection Bandwidth	$\frac {N^2} 4$

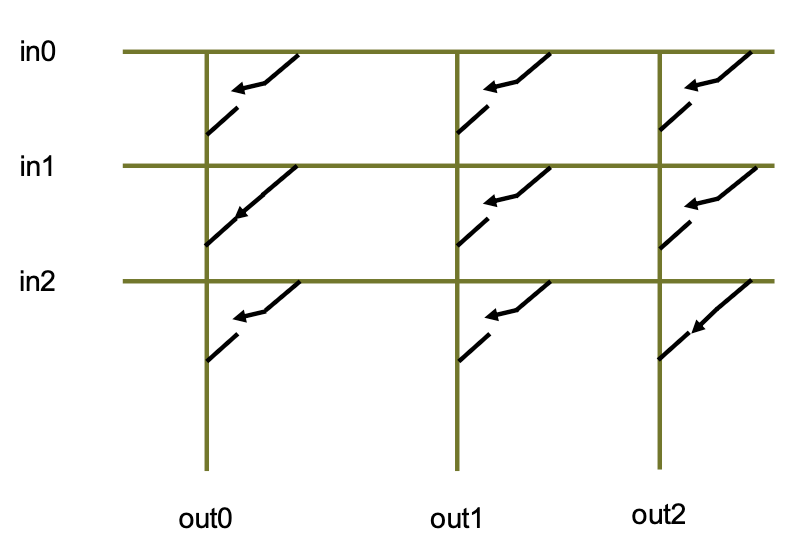
Crossbar

A crossbar switch connects $N$ inputs to $M$ outputs

• At each crosspoint a switch/transistor is either “open” or connects the input to the output line

It’s cheaper than fully connected network: $O(N+M)$ cables vs $O(N*M)$.

It has much better performance than bus network.

• However, area and cost are still quadratic!

Yet the crossbar is a very important building block!

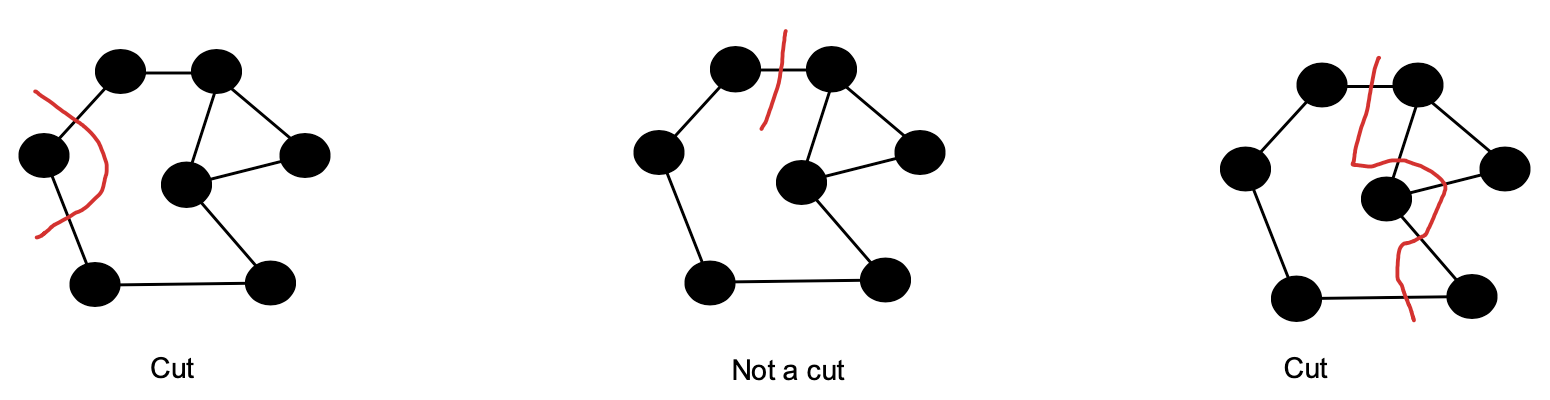
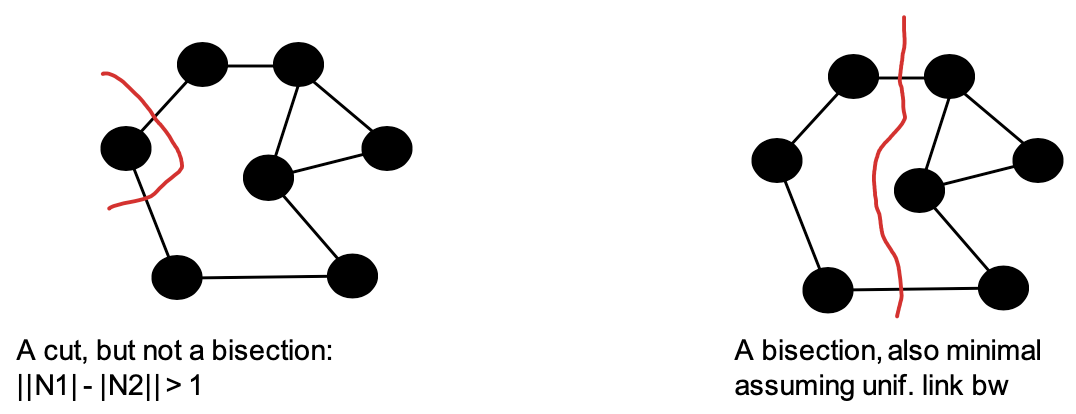
Graph Cuts and Bisection

$V$ is partitioned into $V_1$ and $V_2$ with

\[V_1 \cup V_2 = V\] \[V_1 \cap V_2 = \emptyset\]

for each element in $(u,v)$ in $C$: $u \in V_1$, $v \in V_2$ or vise versa.

Partitioned means that:

Each path from a node in $V_1$ to a node in $V_2$ must contain an edge in $C(V_1, V_2)$

• a.k.a.: How many link failures can the network adapt to?

In networks, each edge (or link, or channel) $e \in E$ has a bandwidth $b_e$

Bandwidth B of the cut:

• Sum of the bandwidths of the cut edges.

\[B(N_1,N_2)=\sum_{c\in C(N_1,N_2)}b_c\]

Bisection of a Network

In networks often $V_1$ and $V_2$ consider terminals separately.

Bisection bandwidth of a network

• Minimum bandwidth of all bisections

In theory, bisection bandwidth tells us the worst-case maximum throughput

• If half of the nodes are senders, half of the nodes are receivers, what is the minimum transfer rate we can achieve?

Why “in theory”?

• Remember Ethernet’s spanning tree protocol?
• Routing / Flow-control are completely ignored!

Effective bisection bandwidth: like BB, but taking routing into account.

Real systems get ~60% of the theoretical BB

Direct vs. Indirect Topologies

Each node in a network can be

• A source or destination for data (also called terminal)
• A switch which forwards packets from input to output ports
• Or both!

Bus and fully connected are direct topologies.

• Each node is directly connected to other nodes, no switches

A topology which contains both nodes and (separate) switches is called indirect topology

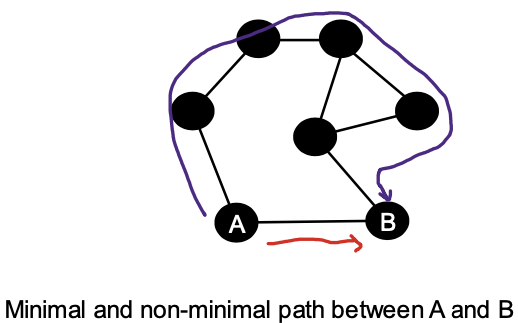
Paths

A path (or route) in a network is an ordered set of channels (edges in graph lingo).

• $P = {c_1, c_2, \dots, c_n}$ where $head(c_i)= tail(c_i+1)$
• Source of $P$: $tail(c_0)$
• Destination of $P$: $head(c_n)$
• Length or hops in a path $P$: \(\|P\|\)

Diameter

The diameter of a network is the largest hop count of the minimal paths for all source-destination pairs. The diameter gives us an indication of the “worst case” latency!

Direct Network Topologies

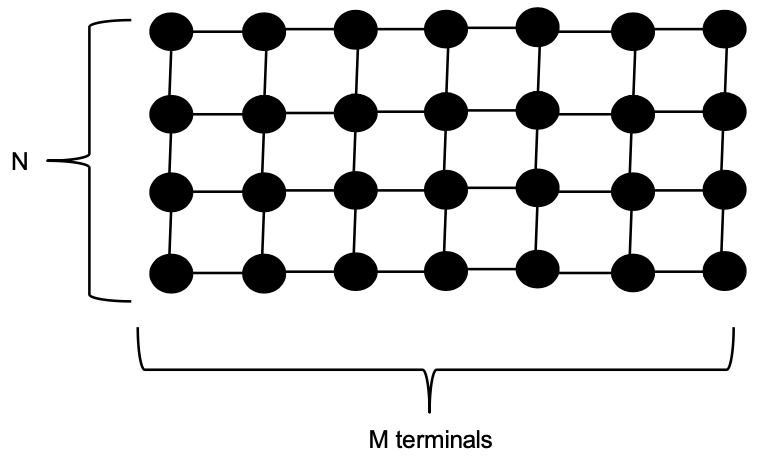
2D-Mesh

Is this a direct or indirect topology?

• Direct, each node is a switch and source/dest

Let’s assume $𝑀 = 𝑁 = 2k$, $P = 𝑀 ⋅ 𝑁$

Property	Value
Degree	$2,3,4$
Diameter	$2\sqrt P$
Total links	$M(N-1)+N(M-1)\approx 2P$
Bisection Bandwidth	$\sqrt P$

In a 2d mesh, the maximum number of paths which do not share a channel/link between any 2 nodes is $4$, because each node as a maximum of $4$ links

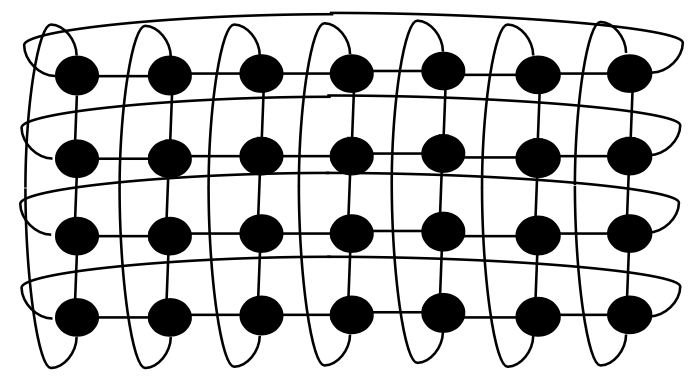
2D Torus

Biggest problem with mesh: high diameter

• We can half the diameter by adding $2\sqrt P$ links

Property	Value
Degree	$4$
Diameter	$\sqrt P$
Total links	$2P$
Bisection Bandwidth	$2\sqrt P$

But wires have vastly different length now.

Indirect Topologies

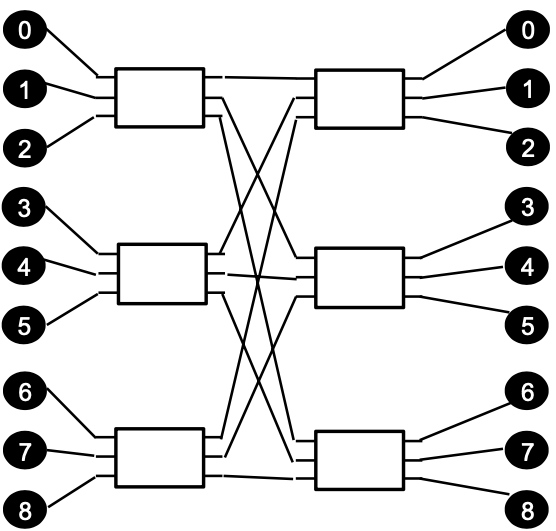
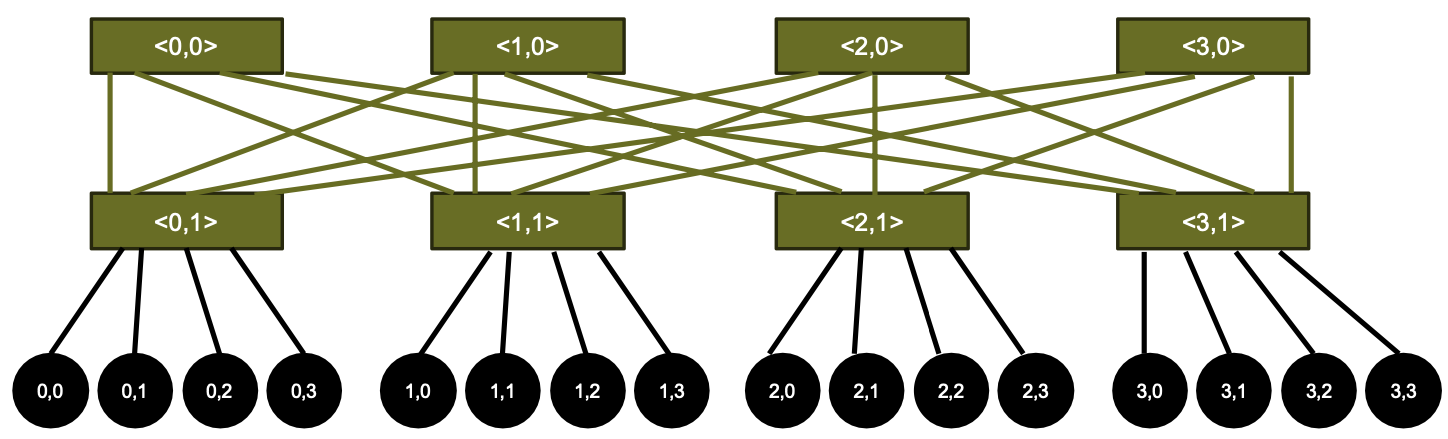
Butterfly

Butterfly networks are also called k-ary n-fly network

They’re composed of $2k^n$ terminals, crossbars of radix $2k$, $n k^{n−1}$ of them

For ease construction: edges are unidirectional, data only flows from left to right

• In reality, source and destination are colocated, we give them the same number.

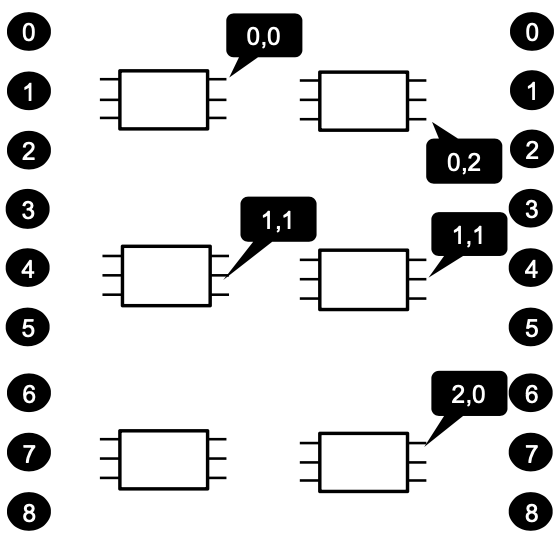
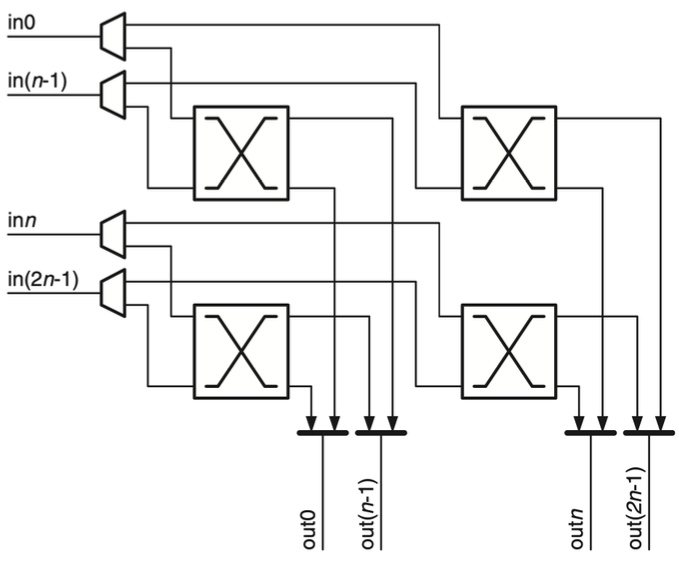
For wiring, label each switch port with an $n$-digit radix-$k$ number $(d_{n−1}, d_{n−2}, \dots , d_0)$ where $d_0$ denotes the port number on the switch, the other digits identify the switch in this stage.

When going from stage $i − 1$ to stage $i$, flip $d_i$ and $d_0$. Wiring of terminals is trivial.

Example $k=3,n=2$

Property	Value
Degree	$?$
Diameter	$n+1$
Total links	$?$
Bisection Bandwidth	$\frac {k^n} 2$

We can construct an arbitrary sized network, given our technology constraint $k$.

Number of nodes	$2n^k$
Total number of switch	$nk^{(n-1)}$
Number of stages	$n$
Switch ports	$2k$, $k$ in, $k$ out

Blocking and Non-blocking Networks

We have seen that in a crossbar and in a fully connected network, any disjoint source/destination pair can communicate independently.

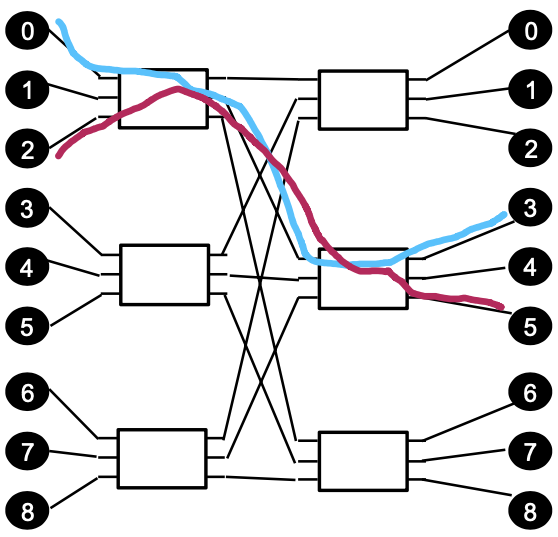
How about our 2-ary 3-fly?

The 2-ary 3-fly is a blocking network

Networks which allow all disjoint src/dst pairs to communicate independently are called non-blocking

You may also hear about non-interfering networks (weaker than non-blocking, makes use of packet switching/buffering)

Non-blocking Indirect Topologies

Bigger Crossbars

Can we built arbitrarily large non-blocking topologies - given that the biggest crossbar we can manufacture in a chip is of limited size?

$4(N\times N)$ crossbars can be used to build a $2N\times 2N$ crossbar

Clos

A Clos network has three stages, and is categorized by three numbers

• $m$ = number of input (output) ports per input (output) switch
• $n$ = number of middle stage switches
• $r$ = number of input (output) switches

How many different paths do we have from one input to one output?

• $M$ paths, we can choose any of the middle switches

The diameter is 4, 2 (within the switch network) + 2 for the two links towards the terminals.

Fat Tree

Idea: Build a tree, make the links at the top “fatter” – but how do we build this using switches with a fixed radix?

• Multiple ways to do this, we show the k-ary-n-tree variant
• $N=k^n$ Terminals, each identified by a $n$ digit number ${0, 1, \dots , k − 1}^n$
• $nk^{n−1}$ Switches, each switch identified by a pair $<w,l>$, where $w ∈ (0, 1, … k − 1)^{ n−1}$ and $l ∈ (0, 1, … , n − 1)$
• There is an edge between a switch $< w_0, … w_{n−2}, n − 1 >$ and terminal $p_0, . . , p_{n−1}$ iff $w_i = p_i$ $\forall i \in (0, … , n − 2)$
• Two switches are connected iff $l = l’ + 1$ and $w_i = w_i’$ $\forall i \neq l$

For example, for a $2$ level Fat Tree built out of switches with $k$ ports:

Diameter $D=4$

Bisection Bandwidth $B=\lfloor\frac {n} 2\rfloor$

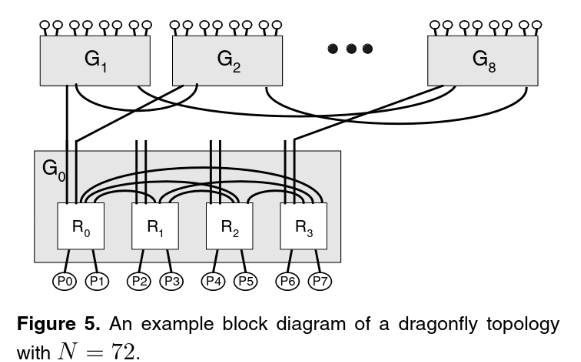
Dragonfly

Idea: Long cables are expensive, separate long and short links

• Consists of fully connected local groups and global links between groups
• One of the most used networks in HPC together with Fat Trees

Slim Fly

Idea: For a fixed switch radix and a fixed diameter, what is the largest network (terminals) we can build?

• Related open problem in graph theory: degree-diameter problem
• We know a bound (Moore bound) for this problem, for many d and k no actual graph which achieves it
• Know some schemes close to this bound, we omit construction rules here (too complicated, based on Galois fields)

The diameter of an indirect slim fly network is 2, but technically it’s 4

Routing

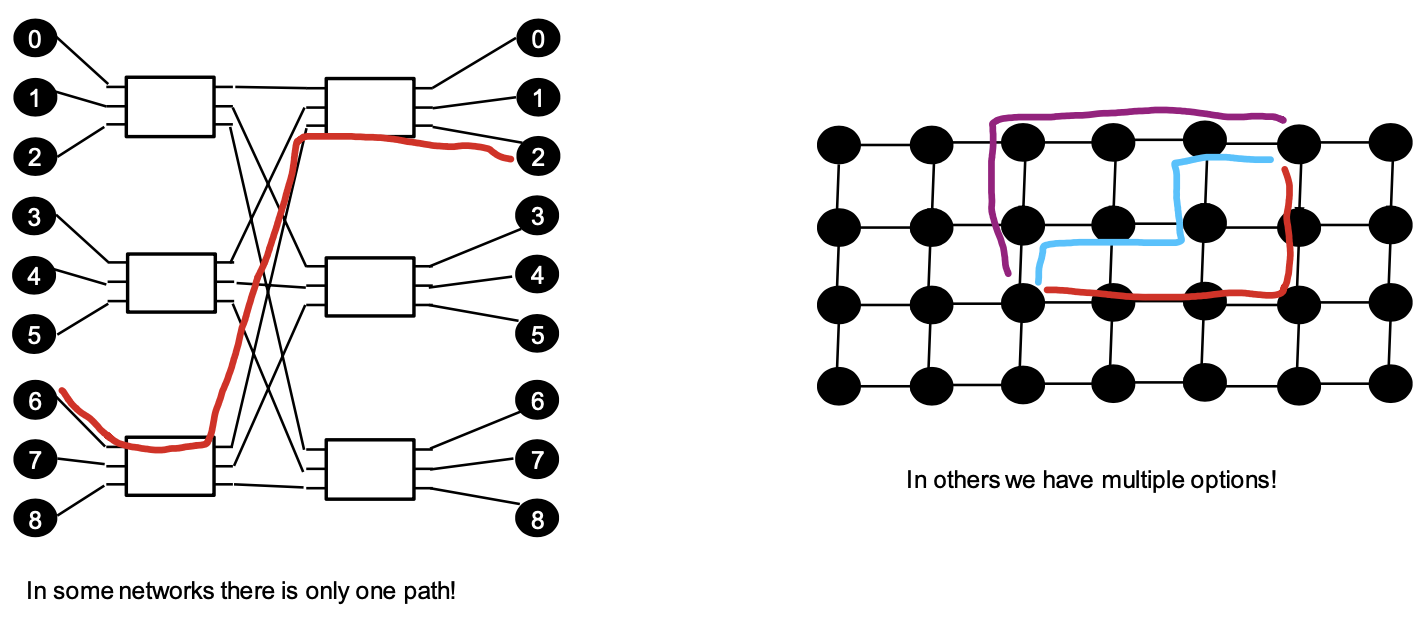
Path Diversity

Topology = existing roads in a city

• Routing tells us which roads to use to get from A to B

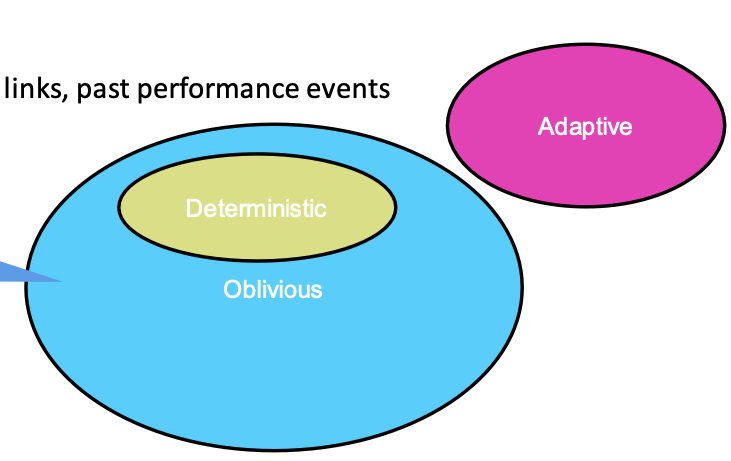
Routing Mechanism Classification

• Deterministic
  • Always choose the same path, regardless of network state
  • Ignores path diversity, BUT easy to implement
• Oblivious
  • Ignores network state
  • Deterministic routing is also oblivious
• Adaptive
  • Adapts to state of the network:
    • Load, broken links, past performance events

Arithmetic Routing

In all regular networks, we can use their construction rule to also determine a possible route

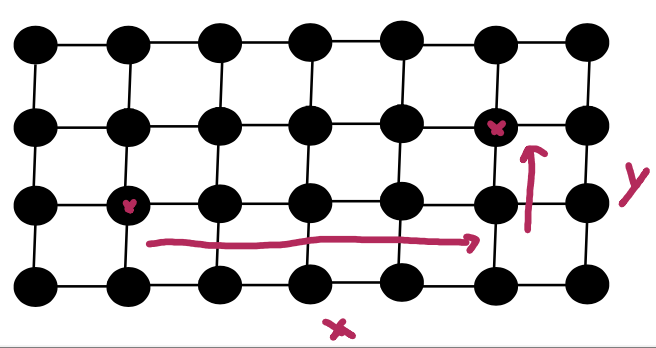
Example: Dimension Order Routing in a Torus/Mesh

• A message $(X,Y) \rightarrow (X’,Y’)$ first travels in the X-direction until its positions’ x-coordinate $= X’$
• Then, it travel in the Y-direction until its positions y-coordinate $=Y’$

Problems:

• Does not take advantage of path diversity, certain links will be > underutilised if traffic is not random
• Cannot react to broken or congested links, single broken link breaks the network

Valiant Routing (A Non-deterministic Oblivious Routing Scheme)

Solves the problem of link-underutilization by choosing a random intermediate destination

• At the cost of network bandwidth and latency

Table-based Routing

The big problem with arithmetic routing is its inflexibility. Instead we can build a huge table:

• For each source and destination list the desired path
• Many extensions are possible here (adding hashes, probabilities for paths, etc.)
• Can split the table and store only the needed portions where required
• Lookups into table need to be fast! $\rightarrow$ Expensive, Scaling issue

Source-based Routing

Instead of making routing decisions in switches, we can add the path of a message to its header

• Increases packet length
• No need for expensive tables in switches

Flow Control Mechanisms

Circuit Switching

• Before any data is sent, allocate a path between input and output ports
• Entire path blocked; setup and teardown takes time
• No buffering needed

Store and Forward

Split message into packets (or flits), send one hop, store, send next hop, …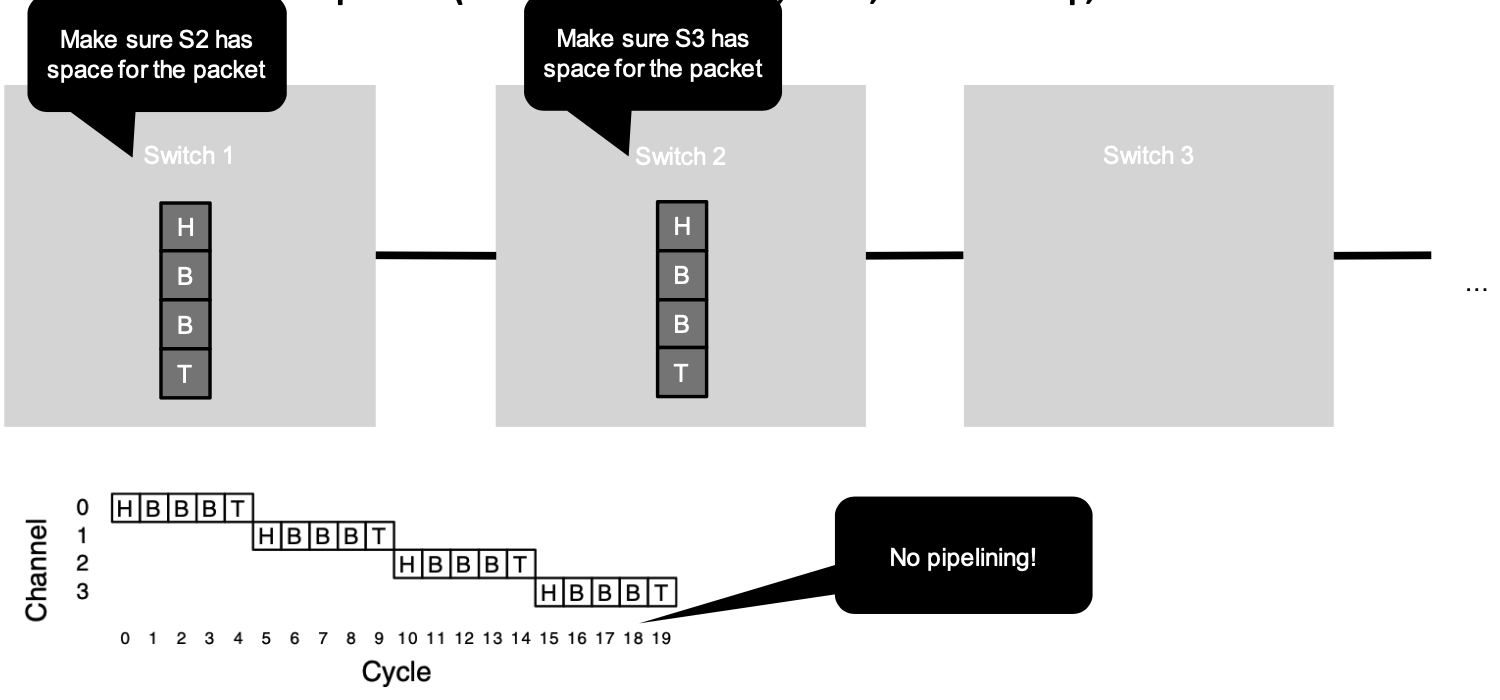

Cut-Through Flow-Control

Send flits in a pipelined fashion, still allocate buffer for entire packet at each hop.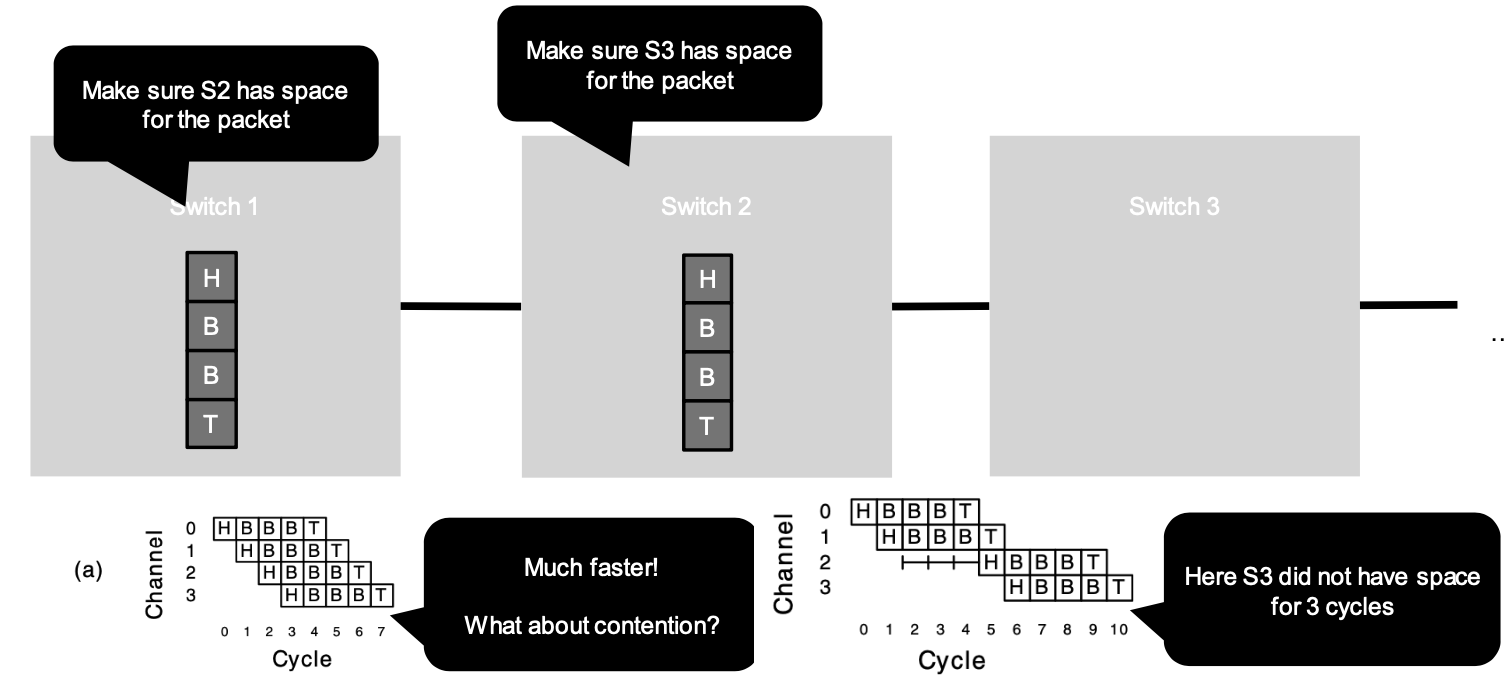

Wormhole Flow-Control

Similar to cut-through, but allocate space for single flit – much more efficient.

• Packets from different src/dst pairs can now interleave
• Switch must remember routing decision of header flit! -> We also allocate “channel state”!
• Can lead to head-of-line blocking, deadlocks!

Resource Allocation

In the previous scenarios, switch we needed to know if switch $i+1$ has resources available. How?

• Credit-based flow-control
• ACK/NACK
• On-Off signalling