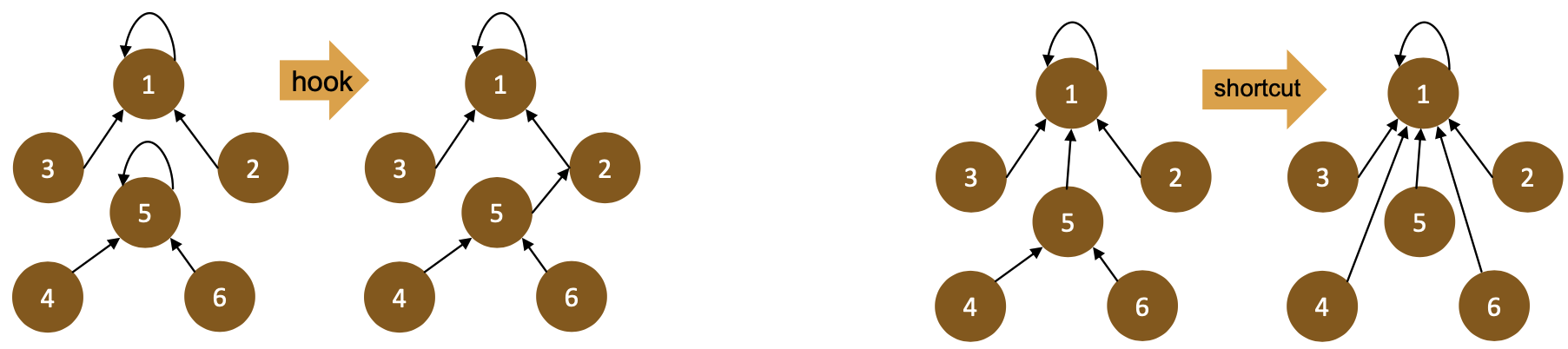Non-oblivious Algorithms

When talking about work and depth, we assume each loop iteration on a single PE is unit-cost (may contain multiple instructions!)

Given: $n$ values in linked list, looking for sum of all values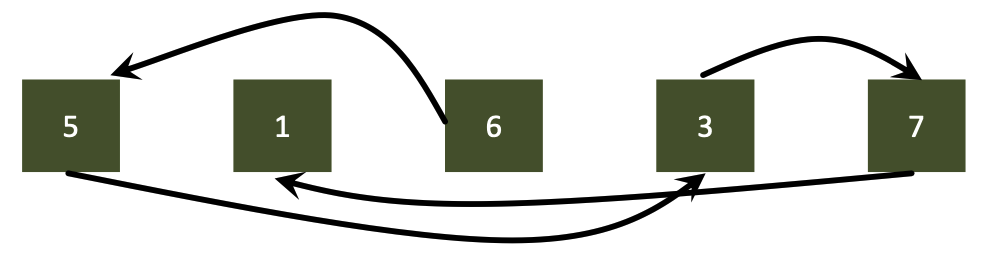

Independent Set

A set $I ⊂ S$ is called an independent set if no $2$ elements in $I$ are connected!

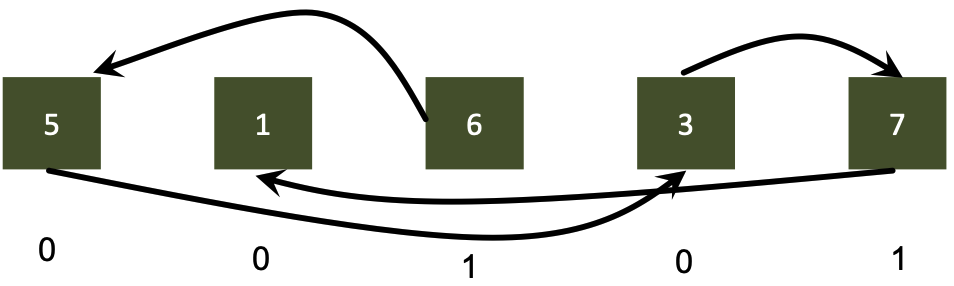
Reduction on a linked list

Sequential algorithm

typedef struct elem {
    struct elem *next;
    int val;
} elem;

set S={all elems}
while (S != empty) {
    pick some i ∈ S;
    S = S - i.next;
    i.val += i.next.val;
    i.next = i.next.next;
}

Parallel algorithm

Basically the same algorithm, just working on independent subsets!

set S={all elems}
while (S != empty) {
    pick independent subset I ∈ S;
    for(each i ∈ I do in parallel) {
        S = S - i.next;
        i.val += i.next.val;
        i.next = i.next.next;
    }
}

Assuming picking a maximum $I$ is free, what are work and depth?

• $W = n − 1$
• $D = ⌈\log_2n⌉$

How to pick the independent set 𝑰?

• That’s now the whole trick!
• It’s simple if all linked values are consecutive in an array – same as “standard” reduction!
  • There, we “compute” (know?) independent sets up-front!

Irregular linked list though?

• Idea 1: find the order of elements → requires parallel prefix sum, D’oh!
• Observation: if we pick $I > \lambda |V|$ in each iteration, we finish in logarithmic time!

Symmetry breaking:

• Assume $p$ processes work on $p$ consecutive nodes
• How to find the independent set?
  • They all look the same (well, only the first and last differ, they have no left/right neighbor)
  • Local decisions cannot be made

Introduce randomness to create local differences!

• Each node tosses a coin → 0 or 1
• Let $I$ be the set of nodes such that v drew 1 and v.next drew 0!
  • Show that $I$ is indeed independent!
  • What is the probability that $v \in I$?
  \[P(v \in I)=\frac 1 4\]

  

Optimizations

As the set shrinks, the random selection will get less efficient

• When $p$ is close to $n ( |S| )$ then most processors will fail to make useful progress
• Switch to a different algorithm: Recursive doubling!

for (i=0; i <= ceil(log2n); ++i) 
    for(each elem do in parallel) {
        elem.val += elem.next.val;
        elem.next = elem.next.next;
    }

Algorithm computes (reverse) prefix sum on the list!

Result:

at original list head we’ll find the overall sum.

---

What are work and depth?

• $W = n⌈\log_2n⌉$
• $D = ⌈\log_2n⌉$

Prefix sum on a linked list

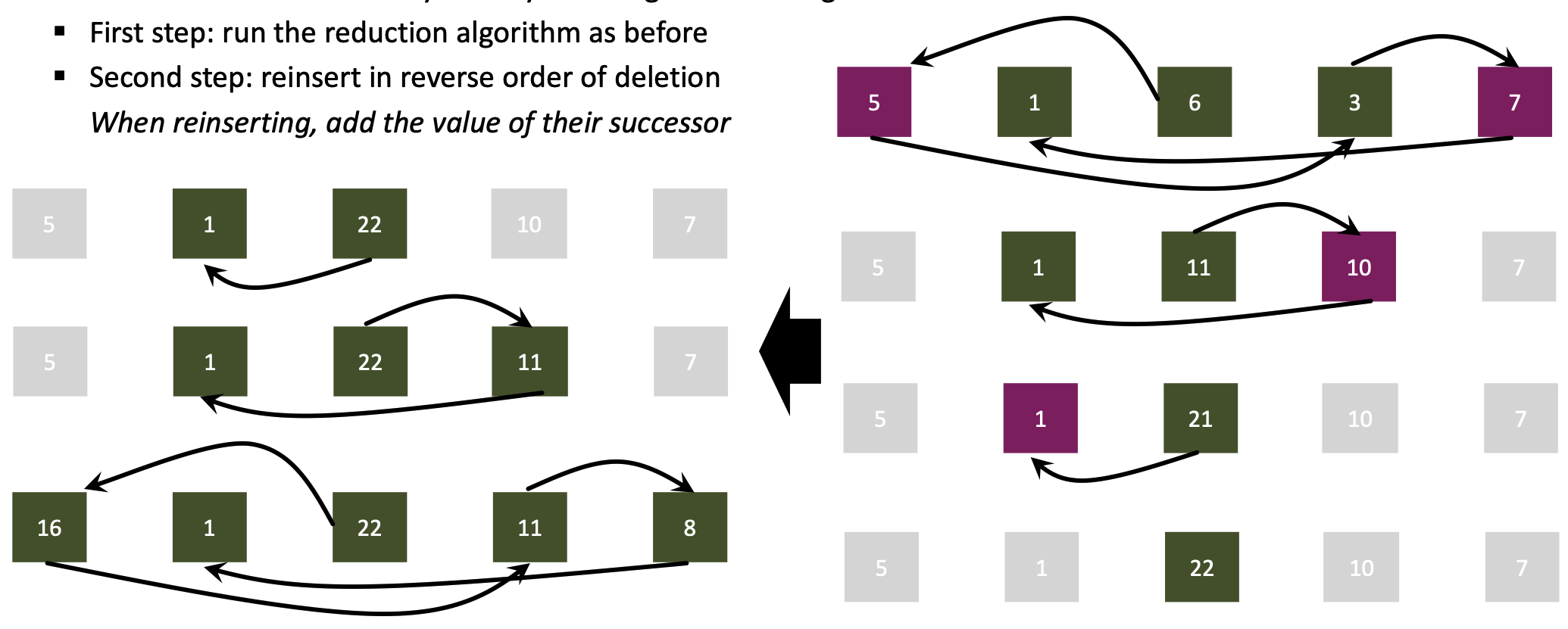
Didn’t we just see it? Yes, but work-inefficient (if $p « n$)! We extend the randomized symmetry-breaking reduction algorithms

1. Run the reduction algorithm as before
2. Reinsert in reverse order of deletion
   • When reinserting, add the value of their successor.

How to implement this in practice?

• Either recursion or a stack!

Nonoblivious graph algorithms - finding connected components

Connected Component

A connected component of an undirected graph is a subgraph in which any two vertices are connected by a path and no vertex in the subgraph is connected to any vertices outside the subgraph.

Each undirected graph $G = (V,E)$ contains one or multiple (at most $|V|$) connected components.

Straightforward and cheap to compute sequentially – question: how?

• Any traversal algorithm in work $O (V + E)$
  • Seemingly trivial
  • Becomes very interesting in parallel
• Our oblivious semiring-based algorithm was $W = O(n^3\log n), D= O(\log^2n)$

FAR from work optimality! Question: can we do better by dropping obliviousness?

1. Initially, each vertex is a (singleton) supervertex
2. Successively merge neighboring supervertices
3. When no further merging is possible → each supervertex is a component

Shiloach/Vishkin’s algorithm

Pointer graph/forest:

• Define pointer array P
  • P[i] is a pointer from i to some other vertex
• We call the graph defined by P (excluding self loops) the pointer graph
• During the algorithm, P[i] forms a forest such that
  • $∀i: (i, P_i)$ there exists a path from i to P[i] in the original graph!

Initially, all P[i] = i. The algorithm will run until each forest is a directed star pointing at the (smallest-id) root of the component

Supervertices:

• Initially, each vertex is its own supervertex
• Supervertices induce a graph - $S_i$ and $S_j$ are connected iff $∃ u, v ∈ E$ with $u ∈ S_i$ and $v ∈ S_j$
• A supervertex is represented by its tree in P

Key components

Algorithm proceeds in two operations:

• Hook – merge connected supervertices (must be careful to not introduce cycles!)
• Shortcut – turn trees into stars
• Repeat two steps iteratively until fixpoint is reached

A fixpoint algorithm proceeds iteratively and monotonically until it reaches a final state that is not left by iterating further

Work and depth?

• $W = O (n^2\log n) , D = O(\log^2n)$ (assuming conflicts are free!)