Work-stealing
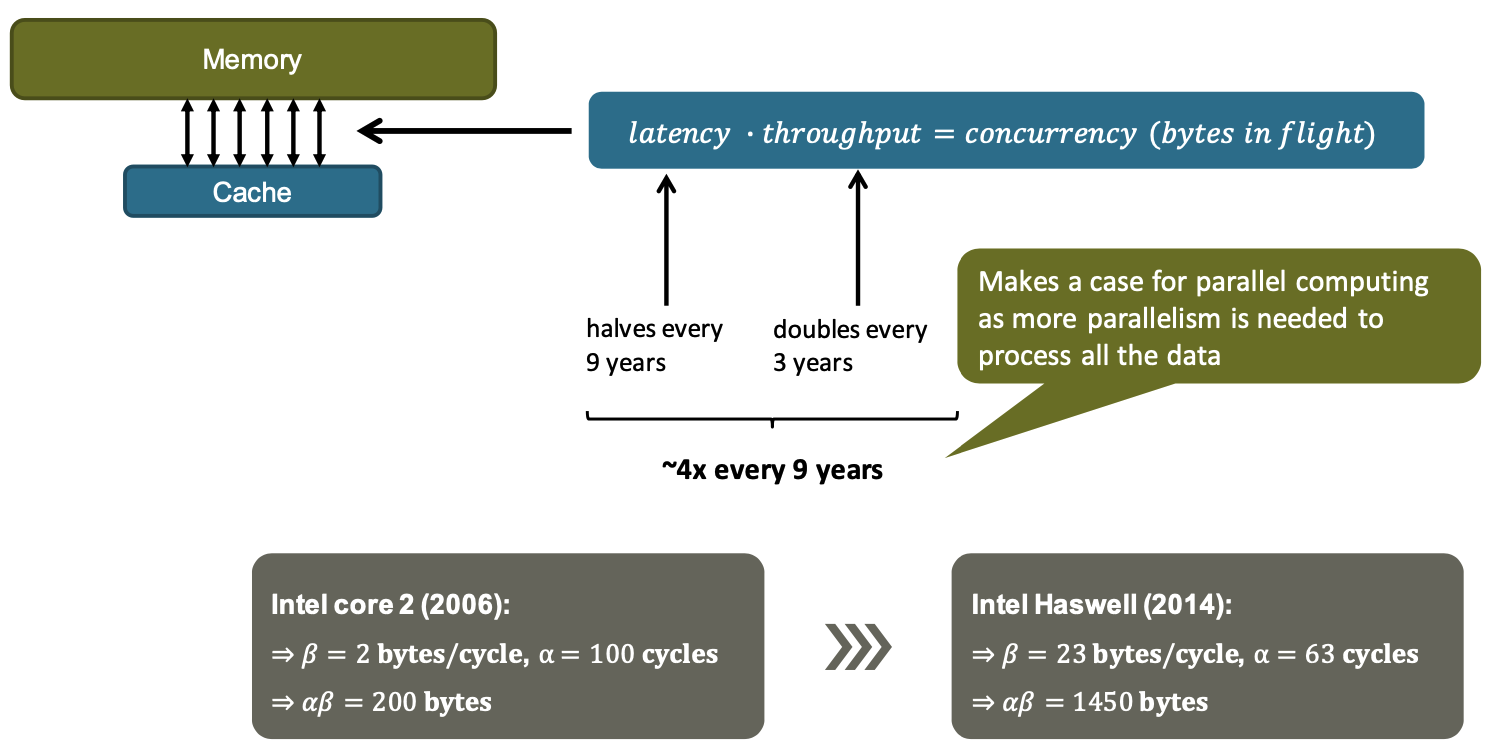
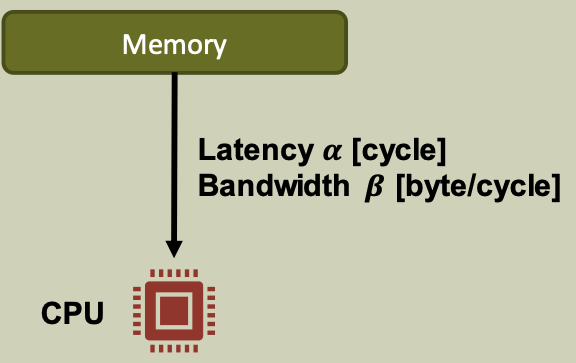
Little’s law
Given a stable system (i.e., input rate = output rate), the long-term average number of items in the system, $𝑁$, is equal to the average throughput, $\beta$, multiplied by the average time an item spends in the system, $\alpha$.
\[N = \alpha \cdot \beta\]Little’s law tells us how much data is in flight.
Example: Memory System
Arithmetic intensity
Given a program P, express number of operations per loaded data.
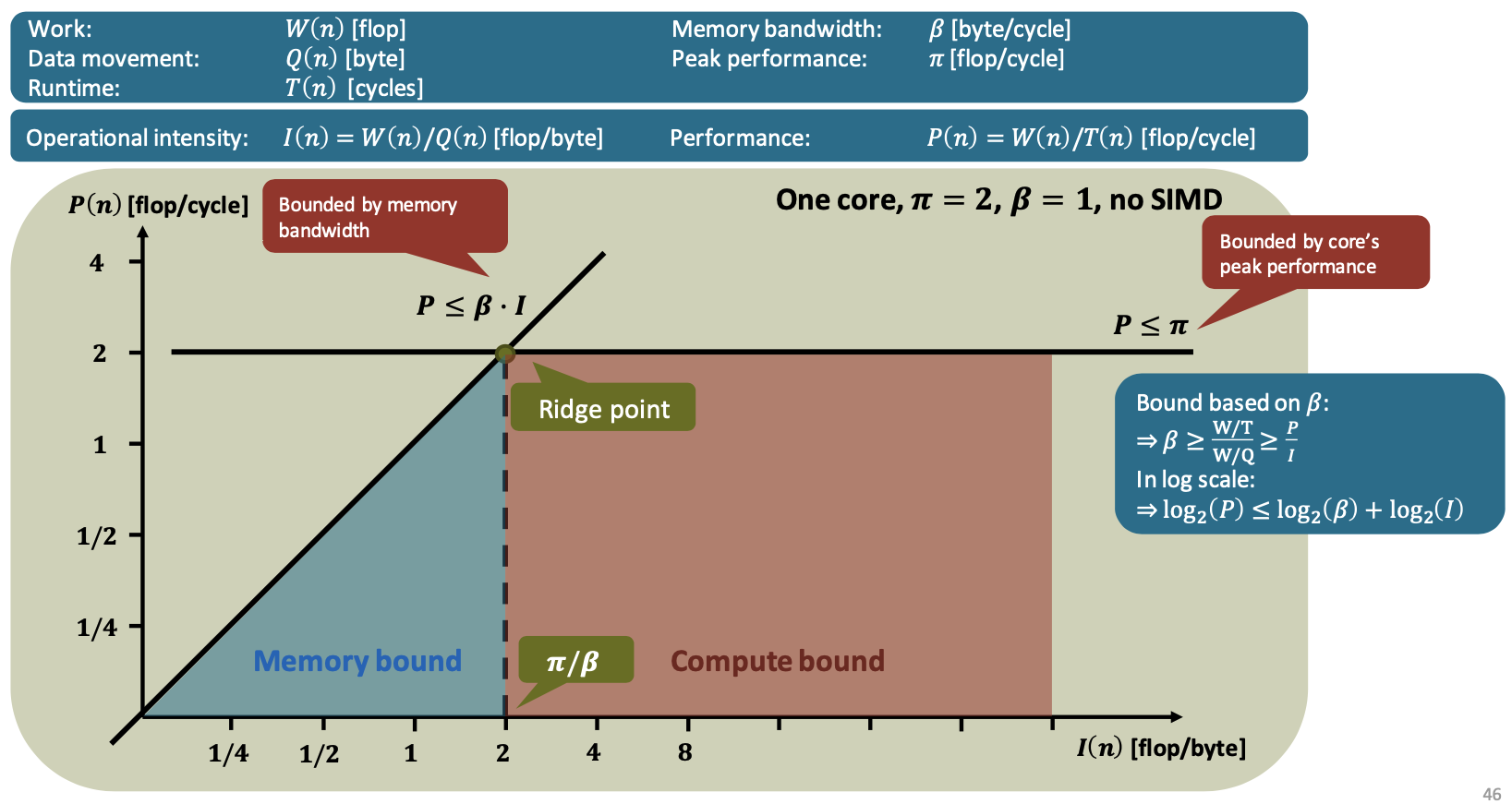
Arithmetic intensity \(A(n)=\frac {W(n)} {L(n)}= \frac {\text{num flops}} {\text{num bytes loaded}}\)
Advantage: very simple to calculate!
- Quite useful for basic algorithmic optimizations (but very limited)
Disadvantage: does not model the effect of a cache/scratchpad
- A cache would be able to serve many loads at highly reduced cost
Operational intensity refines this concept.
Operational intensity
Given a program $P$, assume cold (empty) cache
Operational intensity
\[I(n)=\frac {W(n)} {Q(n)}= \frac {\text{num flops}} {\text{bytes transferred between cache and RAM}}\]
Asymptotic bounds on 𝑰(n)
Assuming only compulsory misses (infinite cache size for simplicity)
| Operation | $I(n)$ |
|---|---|
| Vector sum: $y = x + y$ | $O(1)$ |
| Matrix-vector product: $y = Ax$ | $O(1)$ |
| Fast Fourier transform | $O(\log n)$ |
| Matrix-matrix product: $C = AB +C$ | $O(n)$ |
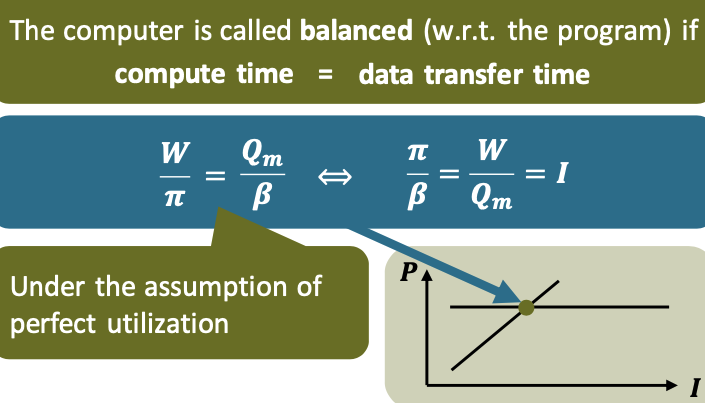
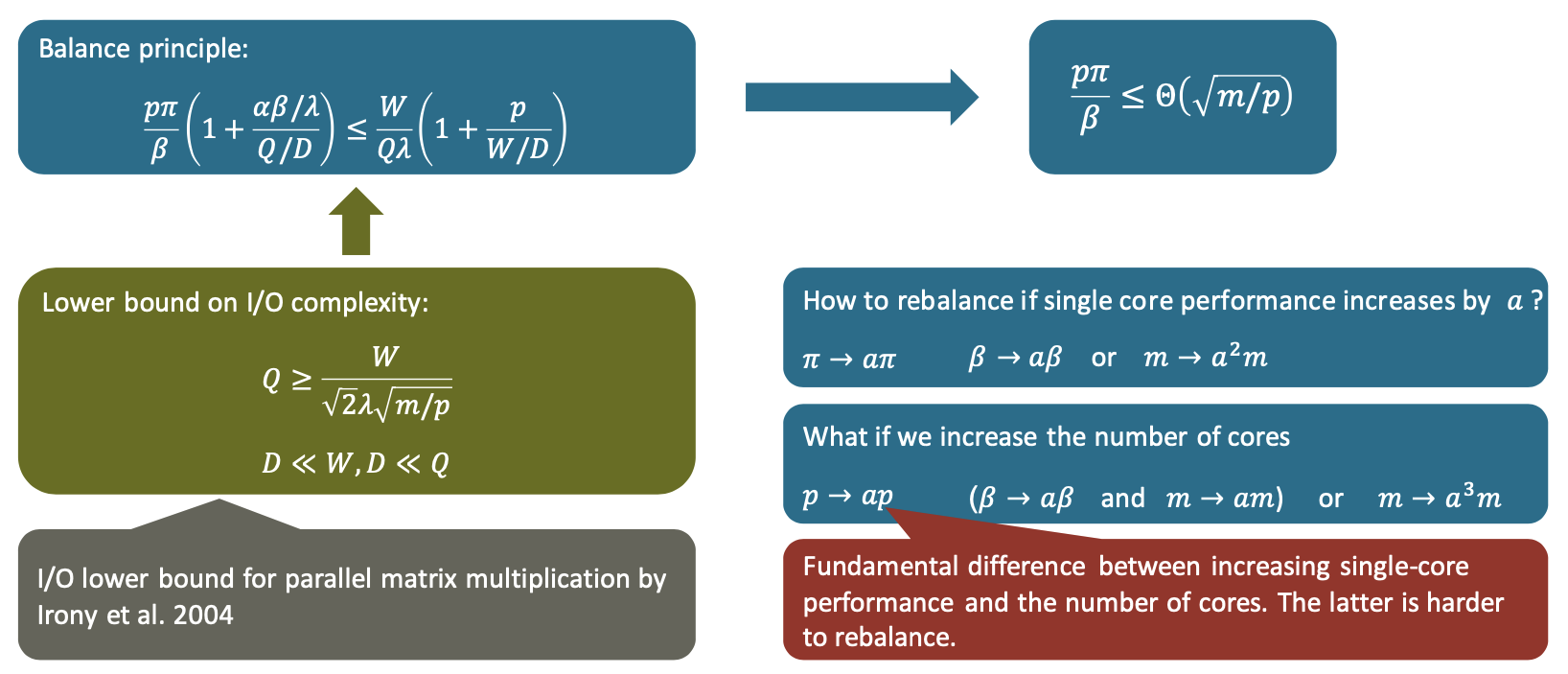
Balance principles I (Kung 1986)
Roofline model
Different optimizations can be represented as performance ceilings ⇒ you cannot break through a ceiling without performing the associated optimization. 
Assume CPU performance $𝜋$ increases by a factor of $a$ (i.e., $a𝜋$), how to rebalance? 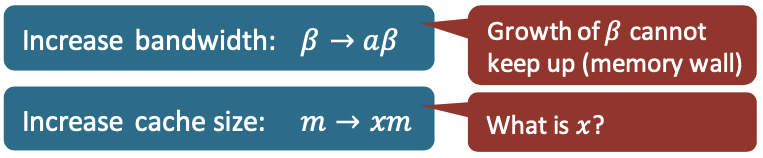
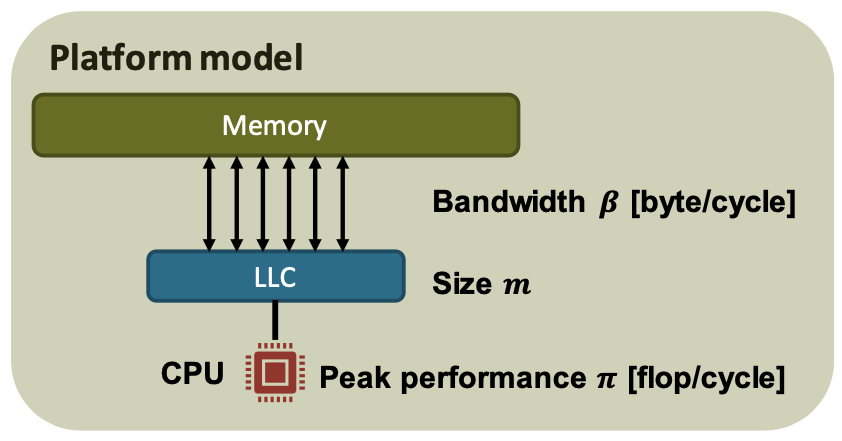
Algorithm/program model
Work: $W$ [number of ops]
Data movement: $𝑄_𝑚$ [byte] (mem cache)
\[\frac \pi \beta = \frac W {Q_m}=I\]How much do we need to increase the cache size, $𝛾$, to balance the increase in CPU performance? 
Alpha-Beta model
Time taken to transfer data of size $n$:
\[T(n) = \frac n \beta+\alpha\]In some literature, $\beta $ describes inverse bandwidth, and the cost of transferring data grows linearly with $n$.
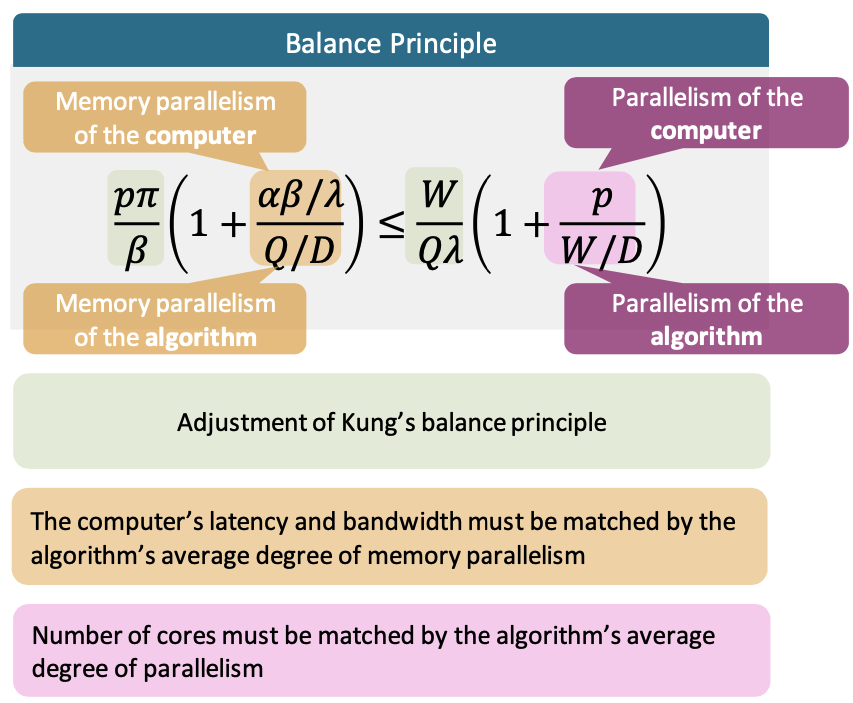
Balance Principles II
Objective: More detailed balance principles for multicores, assessment of hardware trends. 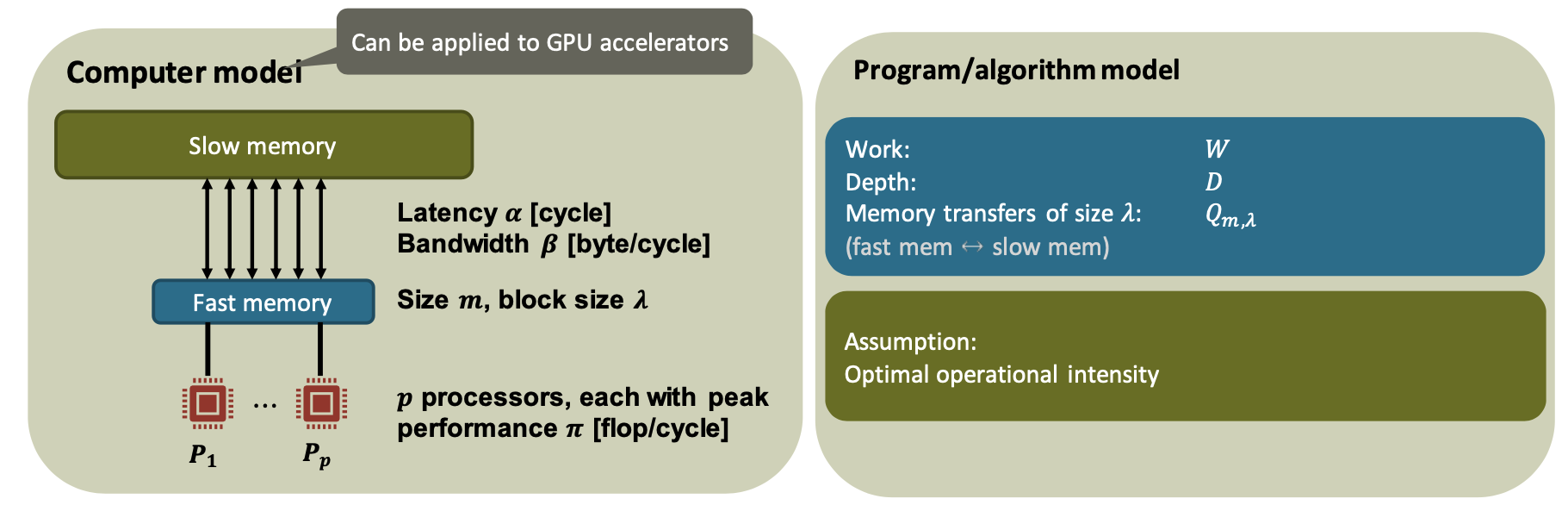
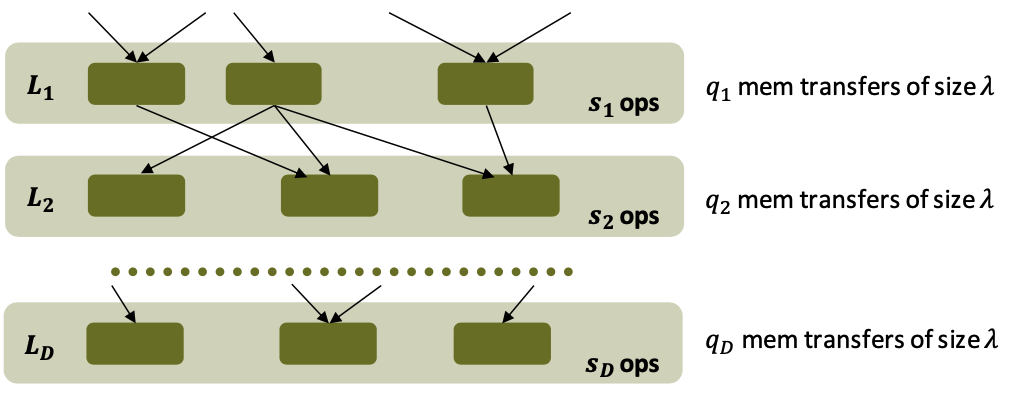
Derivation
Estimate $T_{mem}$ by dividing DAG into levels.
\[Q_{\gamma,\lambda}=\sum^D_{i=1} q_i\]Then, apply alpha-beta model to each level:
\[T_{mem}\approx \sum^D_{i=1}(\frac {q_i \lambda} \beta + \alpha)=\alpha D+ \frac {Q\lambda} \beta\]Brent’s lemma:
\[T_{comp} \approx \frac {D+\frac W p}\pi\]Balance Principle
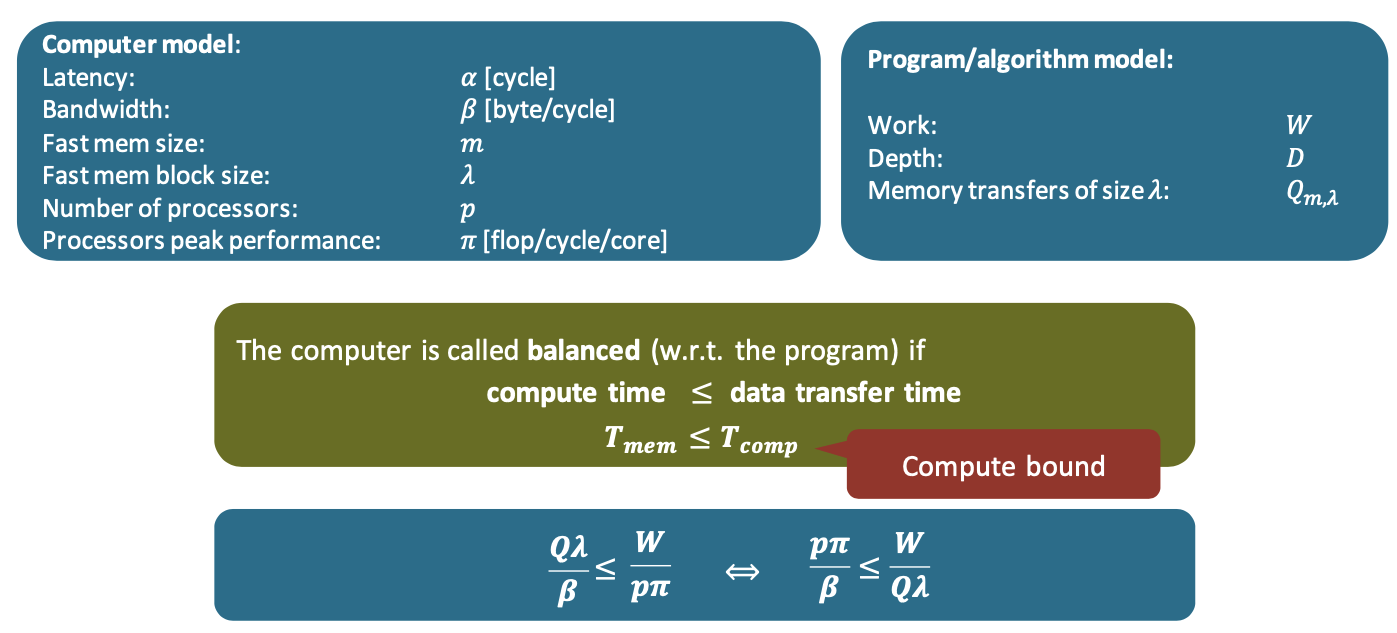
$T_{mem} \leq T_{comp}$
\[\frac {p \pi} {\beta} (1+\frac {\alpha \beta / \lambda} {Q/D}) \leq \frac {W} {Q\lambda} (1+\frac p {W/D})\]